Rock Paper Scissors Lizard Spock
题意:
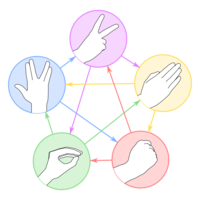
有五种手势,类似于石头剪刀布,有两个串$s, t$,由这五种手势组成,从某个位置开始匹配,如果$t_i$能赢$s_j$得一分,求一个$pos(0\le pos \le len(s)-len(t))$,使得得分最多
Solution:
将上图记为$G$,如果$op_1$可以赢$op_2$,则$G(op_1, op_2)=1$,
枚举可以得分的手势,假设当前手势为$op$,
$$ \begin{aligned} t’_i &=(reverse\ t_i == op ? 1 : 0) \newline s’_i &= G[op][s_i] \end{aligned} $$
将$t’,s’$做卷积,累加每次的结果,再遍历一遍匹配的起始位置,取最大值
#include <cstdio>
#include <stack>
#include <set>
#include <cmath>
#include <map>
#include <time.h>
#include <vector>
#include <iostream>
#include <string>
#include <cstring>
#include <algorithm>
#include <memory.h>
#include <cstdlib>
#include <queue>
#include <iomanip>
#include <unordered_map>
#define P pair<int, int>
#define LL long long
#define LD long double
#define PLL pair<LL, LL>
#define mset(a, b) memset(a, b, sizeof(a))
#define rep(i, a, b) for (int i = a; i < b; i++)
#define PI acos(-1.0)
#define random(x) rand() % x
#define debug(x) cout << #x << " " << x << "\n"
using namespace std;
const int inf = 0x3f3f3f3f;
const LL __64inf = 0x3f3f3f3f3f3f3f3f;
#ifdef DEBUG
const int MAX = 2e3 + 50;
#else
const int MAX = 1e6 + 50;
#endif
const int mod = 1e9 + 7;
#include <complex>
namespace FFT
{
int rev[MAX * 4];
int cnt[MAX * 4];
void fft(complex<double> *a, int n, int inv){
int bit = 0;
while((1<<bit) < n) bit++;
for(int i = 0; i < n; i++){
rev[i] = (rev[i>>1]>>1) | ((i & 1) << (bit-1));
if(i < rev[i])
swap(a[i], a[rev[i]]);
}
for(int mid = 1; mid < n; mid <<= 1){
complex<double> wn(cos(PI/mid), inv*sin(PI/mid));
for(int i = 0; i < n; i += (mid<<1)){
complex<double> w(1, 0);
for(int j = 0; j < mid; j++, w*=wn){
complex<double> u = a[i+j], t = w * a[i+j+mid];
a[i+j] = u + t, a[i+j+mid] = u-t;
}
}
}
}
};
int N;
char s[MAX], t[MAX], rev_t[MAX];
complex<double> a[MAX*4], b[MAX*4];
int mark[100][100];
void init(){
mark['S']['P'] = 1;
mark['P']['R'] = 1;
mark['R']['L'] = 1;
mark['L']['K'] = 1;
mark['K']['S'] = 1;
mark['S']['L'] = 1;
mark['L']['P'] = 1;
mark['P']['K'] = 1;
mark['K']['R'] = 1;
mark['R']['S'] = 1;
}
void solve(char op, int n, int m){
for(int i = 0; i < n; i++)
a[i] = complex<double>(mark[op][s[i]], 0);
for(int i = n; i < N; i++)
a[i] = complex<double>(0, 0);
for(int i = 0; i < m; i++)
b[i] = complex<double>(rev_t[i]==op?1:0, 0);
for(int i = m; i < N; i++)
b[i] = complex<double>(0, 0);
;
FFT::fft(a, N, 1); FFT::fft(b, N, 1);
for(int i = 0; i < N;i++)
a[i] *= b[i];
FFT::fft(a, N, -1);
for(int i = m-1; i <= n-1; i++)
FFT::cnt[i] += (int)(a[i].real() / N + 0.5);
return;
}
int main(){
#ifdef DEBUG
freopen("in", "r", stdin);
#endif
init();
scanf("%s%s", s, t);
int n = strlen(s), m = strlen(t);
N = 1;
while(N <= n+m) N <<= 1;
for(int i = 0; i < m; i++) rev_t[i] = t[m-i-1];
vector<char> ops({'R','P', 'S', 'K', 'L'});
for(auto op : ops){
solve(op, n, m);
}
int ans = 0;
for(int i = m-1; i <= n-1; i++){
ans = max(ans, FFT::cnt[i]);
// printf("%d ", FFT::cnt[i]);
}
// puts("");
printf("%d\n", ans);
return 0;
}